Matriz de Sistema: Lente Gruesa

La posición de la imagen formada por una lente gruesa se puede encontrar utilizando la matriz del sistema. Esto implica multiplicar una forma vectorial de la vergencia incidente, sucesivamente por tres matrices que representan (1) la refracción por la primera superficie, (2) la traslación a la segunda superficie, y (3) la refracción por la segunda superficie. Esas tres operaciones se pueden combinar para formar la matriz del sistema. La vergencia de entrada puede multiplicarse por la matriz del sistema para determinar la vergencia de salida y, a partir de ella, se calcula la distancia de la imagen.

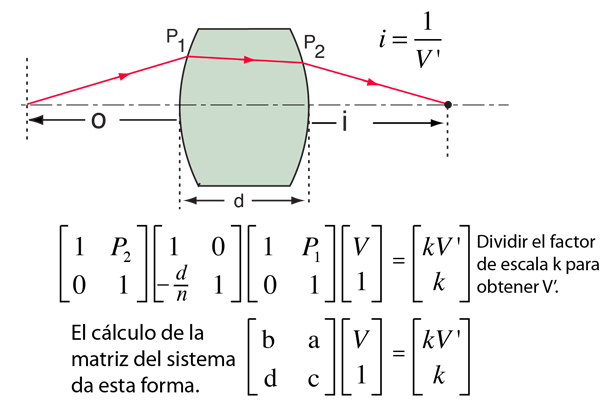
El ejemplo es para una lente con índice de refracción n rodeada por aire (n = 1). Implica las potencias de superficie de la lente y el grosor d entre los vértices. También implica los planos principales H₁ y H₂. Como con la mayoría de las ópticas geométricas ordinarias, es aplicable solo para ángulos pequeños (rayos paraxiales). El desarrollo también sigue la convención de signos cartesianos.

Para vidrio con índice de refracción nlens = n = la potencia de superficie frontal para el radio de lente R1 = m es P1 = m-1 y la potencia de superficie posterior para el radio de lente R2 = m es P2 = m-1 Grosor de lente d = m (Nótese que para una lente convexa doble el radio de superficie frontal R1 es positivo y el radio de superficie posterior R2 es negativo de acuerdo con la convención de signos cartesianos.)

Se utilizarán los símbolos utilizados por Meyer-Arendt para los elementos de la matriz del sistema. b = a = d = c =

**********

A partir de la matriz del sistema se puede calcular una serie de otras características de la lente gruesa.

La mano derecha, o la distancia focal equivalente de la lente es justo el recíproco del elemento de matriz a: f₂ = 1/a = m.

La distancia V₂H₂ desde el vértice derecho al plano principal asociado está dada por V₂H₂= (c-1)/a = m.

La longitud focal del vértice derecho (o longitud focal posterior) está dada por f_v2 = c/a = m.

Nótese que la longitud focal equivalente f₂ es la suma de la longitud focal del vértice posterior y la distancia desde el vértice al plano principal: f₂ = f_v2 + V₂H₂. Existen relaciones similares para el vértice izquierdo o frontal.

La longitud focal del vértice izquierdo (o longitud focal frontal) está dada por f_v1 = -b/a = m.

La distancia V₁H₁ desde el vértice izquierdo al plano principal asociado está dada por V₁H₁= (1-b)/a = m.

La longitud focal frontal equivalente f₁ está dada por f₁ = -(b/a + V₁H₁) = m. **********

Para una distancia de objeto* o = m, el valor de la vergencia de entrada V = . Realizando la multiplicación de matrices indicada a la izquierda da: kV'= k=. Dividiendo ambas por k da la vergencia de salida V' = m-1 de modo que la distancia de imagen i = m

*Usando la convención de signos cartesianos, la distancia del objeto suele ser un número negativo, ya que apunta en dirección opuesta a la dirección de la luz. La vergencia de entrada es por lo tanto negativa (divergente).

La potencia equivalente para la lente gruesa se puede calcular a partir de la ecuación de Gullstrand:

Tenga en cuenta que el cálculo no tiene en consideración el cambio en el grosor de la lente con el ángulo del rayo entrante. Es típico hacer el cálculo solo para los rayos paraxiales donde la desviación del espesor total es despreciable.