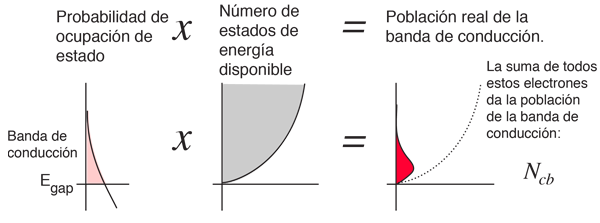
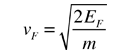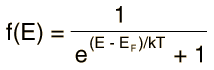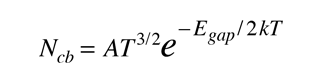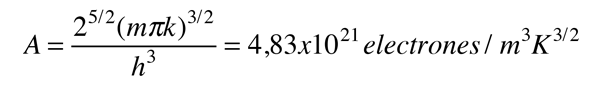El Nivel de Fermi
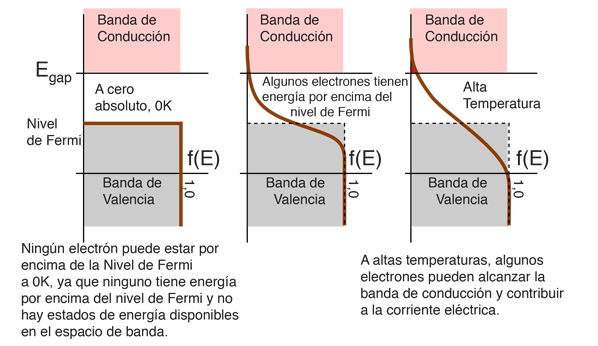
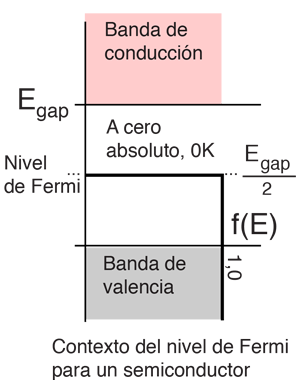
El "Nivel de Fermi" es el término utilizado para describir la parte superior del conjunto de niveles de energía de electrones a la temperatura de cero absoluto. Este concepto proviene de las estadísticas de Fermi-Dirac. Los electrones son fermiones y por el principio de exclusión de Pauli no pueden existir en estados de energías idénticas. En el cero absoluto, estos se encuentran en los niveles mas bajos de energía disponibles de los estados de energía de electrones, constituyendo el llamado "mar de Fermi" ó "líquido de Fermi". El nivel de Fermi es la superficie de ese mar en el cero absoluto, donde no hay electrones que tengan suficiente energía para elevarse por encima de esa suerficie. El concepto de la energía de Fermi es de importancia crucial para la comprensión de las propiedades eléctricas y térmicas de los sólidos. Ambos procesos eléctrico y térmico implican valores de energías de una pequeña fracción de un electrón-voltio. Pero las energías de Fermi de los metales están en el orden de electrón-voltios. Esto implica que la gran mayoría de los electrones no puede recibir energía de esos procesos, porque no existen estados de energía disponibles. Limitado a una pequeña profundidad de energía, estas interacciones constituyen las "ondas en el mar de Fermi".A temperaturas más altas, existirá una cierta fracción caracterizada por la función de Fermi, por encima del nivel de Fermi. El nivel de Fermi juega un papel importante en la teoría de bandas de sólidos. En los semiconductores dopados de tipo p y tipo n, el nivel de Fermi se desplaza por las impurezas, segun lo ilustran bandas prohibidas. El nivel de Fermi se conoce en otros contextos como el potencial químico de electrones.
|
En los metales, el nivel de Fermi proporciona información sobre las velocidades de los electrones que paricipan en la conducción eléctrica ordinaria. La cantidad de energía que se puede dar a un electrón en tales procesos de conducción, son del orden de microelectrón-voltios (ver ejemplo de conductor de cobre), de modo que solamente pueden participar aquellos electrones muy próximos a la energía de Fermi. La velocidad Fermi de estos electrones de conducción, se puede calcular por la energía de Fermi.
Esta velocidad es parte de la ley de Ohm microscópica para la conducción eléctrica. Para un metal, la densidad de electrones de conducción puede deducirse de la energía de Fermi. |
 |
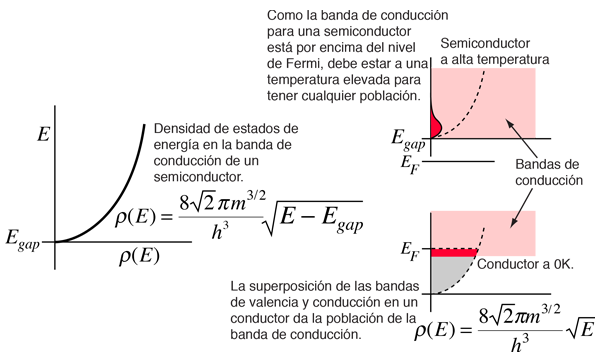
La energía de Fermi también juega un papel importante en la comprensión del misterio de por qué los electrones no contribuyen significativamente al calor específico de sólidos a temperaturas ordinarias, mientras que son contribuyentes dominantes a la conductividad térmica y la conductividad eléctrica. Dado que sólo una pequeña fracción de los electrones en un metal se encuentran dentro de la energía térmica kT de la energía de Fermi, están "congelados" de capacidad calorífica por el principio de Pauli. A temperaturas muy bajas, el calor específico de electrones se convierte en importante.
| Energías Fermi de Metales |
| Tabla de Energías Fermi |
Conceptos de Semiconductor
Semiconductores en Electrónica
| HyperPhysics*****Materia Condensada***** Electricidad y Magnetismo | M Olmo R Nave |