Números Cuánticos y Niveles de Energía Atómica
La solución de los niveles de energía del electrón por el modelo de Bohr o la ecuación de Schrodinger para el hidrógeno, muestran que solamente dependen del número cuántico principal.
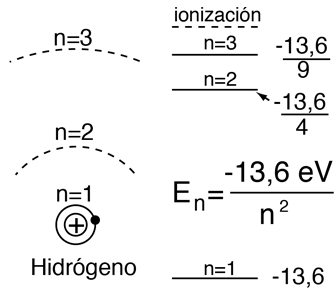
| En el hidrógeno y otros núcleos desnudos con un solo electrón, la energía depende únicamente del número cuántico principal n 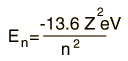 |
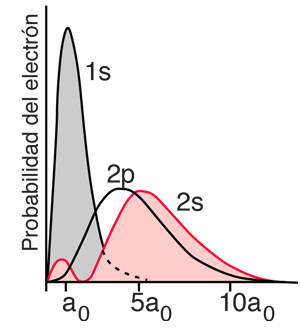 |
En el helio se tiene un par de electrones, y los niveles de energía del helio asociados con un electrón en un estado excitado n = 2, da una dependencia considerable del número cuántico orbital l. Esto se puede atribuir al hecho de que el electrón 2s, penetra más en el interior de la carga del electrón 1s. El electrón 2s está por lo tanto, menos blindado de la fuerza de atracción del núcleo, que el electrón 2p, y tiene inferior energía. Esta dependencia del número cuántico orbital de un simple electrón en estado excitado, es responsable de la penetración de la función de onda, y se puede ver claramente en los niveles de energía de los metales alcalinos, tales como el sodio y el litio. |
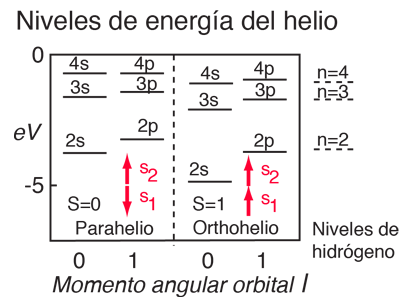 |
Otro efecto sobre los niveles de energía del helio, puede estar asociada con el número cuántico de espín, y se deriva de los requisitos de simetría del principio de exclusión de Pauli. Téngase en cuenta que para valores dados de números cuánticos principal y orbital, los estados con espines paralelos son significativamente más bajos que aquellos con espines anti-paralelos. Esto es referido a veces como el efecto espín-espín, y se resumen en la regla de Hund #1. |
En los átomos ligeros con múltiples electrones exteriores a una capa completa, se pueden combinar los momentos angulares orbitales, para dar un momento angular resultante L. Considerando el modelo vectorial, se espera poder obtener diferentes valores de L, para un determinado conjunto de momentos angulares orbital individual. Resultando que el valor L más grande posible, tiene la menor energía. Esto es referido a veces como el "efecto órbita-órbita" (regla de Hund #2)
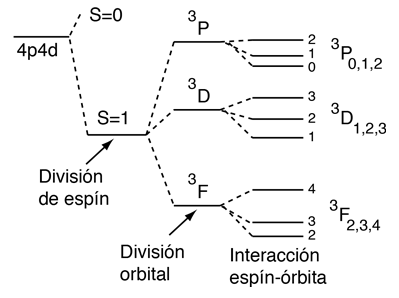 |
Con múltiples electrones, hay una fuente adicional de desdoblamiento de los niveles de energía de los electrones, que se caracteriza en términos de otro número cuántico, el número cuántico del momento anglular total J. Al origen del desdoblamiento se le llama efecto espín-órbita.En los átomos ligeros, los momentos angulares de espín y orbital de los electrones individuales, interactuan entre sí con suficiente fuerza para combinarse y formar un espín resultante S, y un momento angular orbital resultante L (esto se llama acoplamiento Russell-Saunders o LS). El espín S y el momento L se combinan, para producir un número cuántico de momento angular total J, y se tiene que los valores más altos de J, corresponden a menores energía (regla de Hund #3) |
Cuando se aplica una interacción externa tal como un campo magnético, se producen desdoblamientos adicionales de los niveles de energía, y ese desdoblamiento se caracteriza en términos del número cuántico magnético, asociado con la componente z del momento angular. Este desdoblamiento se llama efecto Zeeman. El efecto sobre los niveles de energía de los campos eléctricos aplicados, se llama efecto Stark.
| Niveles de Energía de Átomos Multielectrónicos |
Conceptos de la Ecuación de Schrödinger
Conceptos del Hidrógeno
Conceptos de Estructura Atómica
| HyperPhysics*****Física Cuántica | M Olmo R Nave |